基本图形再挖掘——2024年湖北省中考模拟数学第23题
万众瞩目的2024年湖北省中考模拟数学(非武汉地区)卷,整体难度较低,这是面对全省各地区过大的差距进行的一种妥协,在难度分布上,仍然依照“斜锯齿”原则进行了调整,其中选择题第10题和填空题第15题相对略有提高,第23题较为平和,第24题最后一问难度较高。
和武汉地区的几次元调模拟卷相比,第23题几何综合的难度大大降低了,体现了有别于武汉地区的命题风格,本题取材于课本习题,基调是旋转全等,融入了轴对称、勾股定理等,对学生观察图形能力提出了较高要求,受困于第3问的学生,多数原因是图形间的关联未能找到,或者说平时课堂学习中,观察图形的培养存在较大问题,这在后期教学中值得注意。
题目
在Rt△ABC中,∠C=90°,将△ABC绕点A顺时针旋转得到△ADE,旋转角小于∠CAB,点B的对应点为点D,点C的对应点为点E,DE交AB于点O,延长DE交BD于点P.
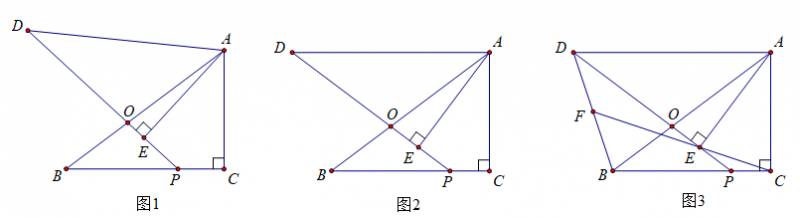
(1)如图1,求证:PC=PE;
(2)当AD∥BC时,
①如图2,若CA=6,CB=8,求线段BP的长;
②如图3,连接BD,CE,延长CE交BD于点F,判断F是否为线段BD的中点,并说明理由.
解析:
(1)基本思路连接AP构造全等,利用旋转前后两个三角形全等,得到AE=AC,再加上公共边AP,得Rt△APE≌Rt△APC,所以PC=PE,如下图;
(2)①新增条件AD∥BC后,事实上整个图形是静态图形,我们可得到∠DAO=∠B,同时由于旋转全等,∠B=∠D,于是∠DAO=∠D,即等腰△AOD;
当CA=6,CB=8时,首先可得它们的对应边AE=6,DE=8,在Rt△AOE中,我们设法表示出其三边长,再利用勾股定理列方程即可,设OA=OD=x,则OE=8-x,由OA²=OE²+AE²,得方程x²=(8-x)²+36,解得x=25/4;
仍然由AD∥BC可证明等腰△BOP,并且利用前面求得的x,先求出OE=8-25/4=7/4,再求出OB=AB-OA=10-25/4=15/4,于是OP=OB=15/4,所以PE=OP-OE=15/4-7/4=2,则PC=PE=2,最后BP=BC-PC=8-2=6;
当然本题也可以利用相似来完成,但对于本次省考模拟的考试范围,超纲了,简略说明如下:△AOD∽△BOP,且相似比为5:3,所以求得BP=6;对于学生使用此方法完成,个人意见是不予全分,以免滋生超纲学习的不正之风;
②作为本题难点,关键是识图,在前面结论中PC=PE,说明△PCE为等腰三角形,恰好还有条件AD∥BC,所以当我们延长CF、AD交于点G,便可得到另一个等腰△DEG,如下图:
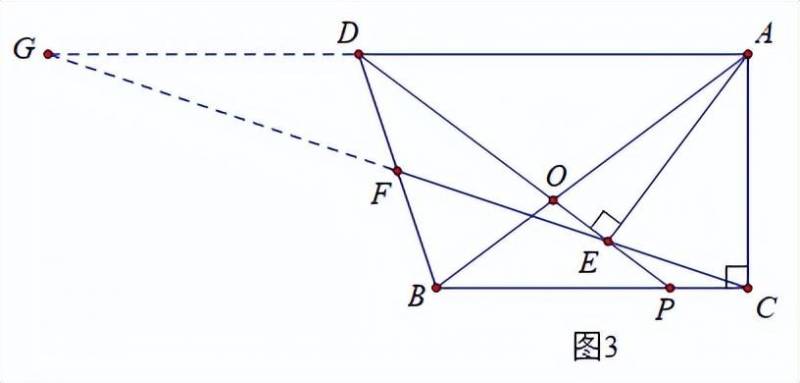
若想证明点F为BD中点,则需要证明△DFG≌△BFC,它们在平行线间,所以相等的角众多,我们重点寻找边相等的条件;
从旋转全等中可得DE=BC,再加上等腰△DEG中DE=DG,于是DG=BC,全等条件已经齐备,于是△DFG≌△BFC,得DF=BF,即点F为线段BD中点.
解题思考:
本次模拟省考的考试范围在考前广泛征求过意见,最终确定为七年级、八年级以及九年级上册内容,从整卷命题中也能发现,严格遵循了上述范围要求,当然由于初中数学各章节的关联紧密,不可避免地会出现能够使用九年级下册的知识去解题,所以对于阅卷标准提出了较高要求,仁者见仁,智者见智吧!
从学生实际答题体验来看,很多中等生完成前面基础部分毫无压力,只是在第10题和第15题消耗了较多时间,而这两道题中第10题是可以利用函数图象性质秒杀的,第15题是可以大胆猜想特殊三角形的,这都在一定程度上提供了“捷径”,只是这个捷径要想走通,需要平时对数学知识的深度理解,浅一点都不行,这就有效地区分出了中等生和学霸,耗时长且正确率不稳定的基本上是中等生,学霸基本可以做到秒杀。
第23题与传统武汉几何综合存在不小差距,首先是难度,以元调模拟题为对照,确实小儿科,没有设置高门坎,在目前难度下要想获得较好的区分度,很不容易,如果拿到武汉地区考生,可能本题满分人数会大大增加,造成优分层的混淆;其次是数学思想,本题3个小题间关联较弱,几乎可以看作相互独立的问题,与武汉几何综合相比,方法迁移基本看不出来,反倒是给学生不断搭梯子,给人感觉是很小心地设置条件和结论,生怕难度超标,心疼一下命题专家们。
最后,第23题在重重限制之下,仍然让中等生感觉到了“难”,这是正确的命题思路,未来真正的省考,想必不会戴上如此枷锁,所以更大的考验,在六月。
微信公众号:爱数学做数学