怎样打响指，掌握这个技巧让你更自信

在《复仇者联盟4》中，当众多超级英雄面对灭霸的大军，难以招架之时，钢铁侠抓住了奇异博士所预言的千万分之一的机会，打响响指，牺牲自己，拯救了宇宙中一半的生命。这一个响指是英雄史诗式的，同时也为钢铁侠这一人物形象画上了圆满的句号。

实际上，几千年来， 打响指 这一动作一直存在于人类文化中，古人通常将其作为一种交流和音乐的形式进行使用。最早的关于打响指的记载可以追溯到公元前320年的希腊，那里的一件陶器描绘了荒野之神，蜷缩起右手打响指的姿势（图1a）。

此外，古希腊人普遍使用打响指来打节拍。然而，响指并不局限于一种文化。它在创造尖锐声音方面的简单性和有效性已被纳入许多文化中，包括西班牙的弗拉门戈舞，以及众多的影视作品当中。今天，响指更是具有广泛的应用，例如打招呼的手势（类似于握手），用于多个麦克风的同时定位，用于盲人的回声定位，或用于数字设备的生物识别认证。

鉴于此， 佐治亚理工学院 M. Saad Bhamla团队 利用高速摄像和力传感器，对打响指的工作进行了动力学分析，揭示了皮肤摩擦力的核心作用 。

作者还开发了一个 基于摩擦力的柔性可压缩闩锁介导的弹簧驱动模型，并进一步阐明摩擦力与可压缩闩锁的相互作用。 该工作揭示了表面之间的摩擦力对闩锁系统的调控作用，并 为许多机器人和超快速能量释放结构中基于摩擦力的复杂设计提供了一定的启示作用。 该研究以题为“The ultrafast snap of a finger is mediated by skin friction”的论文发表在最新一期《Journal of the Royal Society Interface》上。11月17日，该论文被Nature以“It’s a snap: the friction-based physics behind a common gesture”为题，作为亮点报道。

【打响指过程的动力学分析】

作者利用高速摄像和力传感器，分析了打响指的动力学状态。通过放置在中指和拇指之间的触觉压力传感器进行力的测量，并利用高速摄影机在手腕、指节和指尖上的各点之间进行角度测量，作者发现， 打响指的动作在7毫秒内达到了1.6×106°s-2的峰值角加速度。 接着，作者在拇指和中指上覆盖不同的材料以产生不同的摩擦系数和不同的可压缩性，揭示了皮肤摩擦力的核心作用，并将打响指动作抽象成一个闩锁介导的弹簧驱动（ ，LaMSA）系统。

图1. 打响指是一个三相的、以一维为主的运动，具有超高的速度和加速度。(a) 一件公元前320-310年的陶器，描绘了希腊的野性之神潘，打响指的姿势。(b) 从侧面看，打响指不同时间点的运动的综合图像。(c) 响指的运动学和动力学。(d) 从正面拍摄的打响指照片。

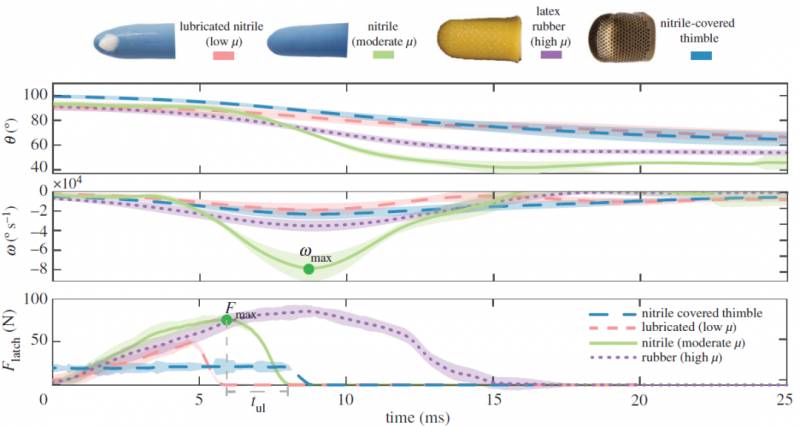
图2. 摩擦和压缩对打响指的影响。手指覆盖在润滑的丁腈橡胶（低μ，粉红色）、丁腈橡胶（中等μ，绿色）、乳胶橡胶（高μ，紫色）和丁腈橡胶顶针（低接触面积，蓝色）上的角位移、速度和法向力

作者发现， 当拇指和手指之间的表面摩擦适中时，可产生最高的速度和加速度。 用Fmax表示储存在手指系统内生理弹簧所受的力的大小。Fmax随不同摩擦面发生如下变化。当摩擦系数μ越大，上述弹簧中可储存的力就越大。作者将tul定义为两个手指从第一次运动开始的接触时间，它是衡量因摩擦而损失多少能量的一个良好指标。tul随着μ的增加而增加，表明随着摩擦的增加，更多的能量被损耗。实验结果表明， 使用丁腈橡胶作为接触面的最大速度ωmax最高，与润滑丁腈橡胶（低μ）和乳胶橡胶（高μ）相比，它的摩擦系数适中。

图3. 拇指和手指之间适中的表面摩擦可产生最高的速度和加速度。(a) Fmax随不同摩擦面的变化。(b) tul随不同摩擦面的变化。tul被定义为两个手指从第一次运动开始的接触时间，因此是衡量因摩擦而损失多少能量的一个良好指标。(c) ωmax随不同摩擦面的变化。

【打响指过程的模型建立】

作者将打响指的过程抽象为闩锁介导的弹簧驱动（LaMSA）系统。LaMSA系统是指在一个相对较长的时间内，能量被外部电机加载到质量弹簧系统中，然后被锁扣固定住。 当闩锁被迅速释放时，就实现了超高速运动，使储存的势能在相对较短的时间内爆炸性地发射物块。

在打响指的过程下，作者假设手臂肌肉为马达，在手指和手臂的肌腱作用下加载势能，这些肌腱就像弹簧一样（图1b）。中指和拇指之间的皮肤摩擦力有助于中指的锁定，但也阻碍了解锁和运动，在打响指的动态过程中起着双重作用。系统在最开始时，弹簧被压缩，负载和闩锁位于θ0的角度。当解锁电机作用于锁扣时，系统就会移动，导致负载在正Y方向加速，直到达到解锁时间，也就是锁扣和负载最后一次接触的时间。在这之后，负载继续加速，完全是由于弹簧的力量，没有其他力量作用于它。这种情况一直持续到解锁时刻，也就是达到弹簧平衡位置的时候。在这一点上，负载继续移动，没有任何外力。

图4. 打响指的模型是一个一维闩锁弹簧系统。(a) 打响指的示意图。(b) 类比于传统的锁存器介导的弹簧驱动系统。(c) 这些示意图展了该系统随时间的演变。

【模型结果的分析】

作者研究了在最佳摩擦系数μ的情况下产生最大的初始速度。在系统解锁前，负载的质量不断增加。在系统解锁之后，负载质量遵循简单的谐波运动，直到达到最大速度，达到这一个点后，它从弹簧上脱离，并以这个速度继续运动。该模型显示 最佳的μ为0.20 ，当μ低于或高于该值时，最大速度会下降。而作用在负载质量上的法向力在减少到零之前从最大值缓慢下降。前面提到的最佳μ产生最低的tul，而较低和较高的μ会导致较高的tul。该模型的结果与实验趋势一致。

作者通过能量分析，确定该最佳的μ可以被应用于任何通用的系统，从而使该分析适用于其他基于摩擦的LaMSA系统。图6显示的是负载K达到的最大动能（黑线），初始弹簧势能U（蓝色），以及模型中每个点μ的能量耗散Ed（红色）。随着μ的增加，初始弹簧势能U增加，直到达到系统的最大存储能力，而最大动能Kmax在减少之前达到一个峰值。作者计算了现象学模型的势能和耗散的能量相对于μ的导数（dU/dμ和dEd/dμ）。可以看出，K的峰值发生在dU/dμ和dEd/dμ相交的μ处， 这一点标志着系统从加载主导的模式过渡到耗散主导的模式。